Il s'agit dans ce cas d'étudier le refroidissement d'une plaque 2D soumise à des conditions de Dirichlet sur ses quatre cotés et initialement à une température uniforme.
1er cas:
(C.L): T(0,y,t) = 0 ; T(1,y,t) = 0 ; T(x,0,t) = 0 ; T(x,1,t) = 0.
(C.I): T(x,y,0) = 1.
Le solveur "laplacianFoam" est utilisé en modifiant l'exemple de la barre 1D au niveau du fichier "blockMeshDict" et des conditions aux limites.
|
|
|
|
|
|
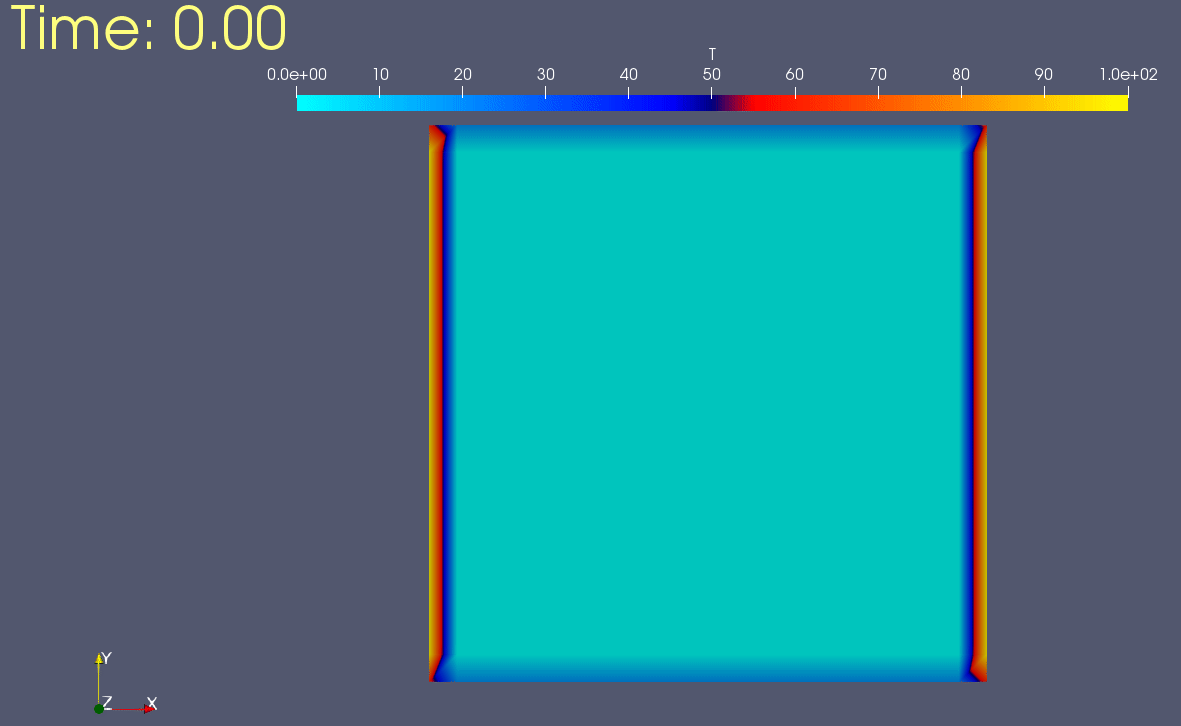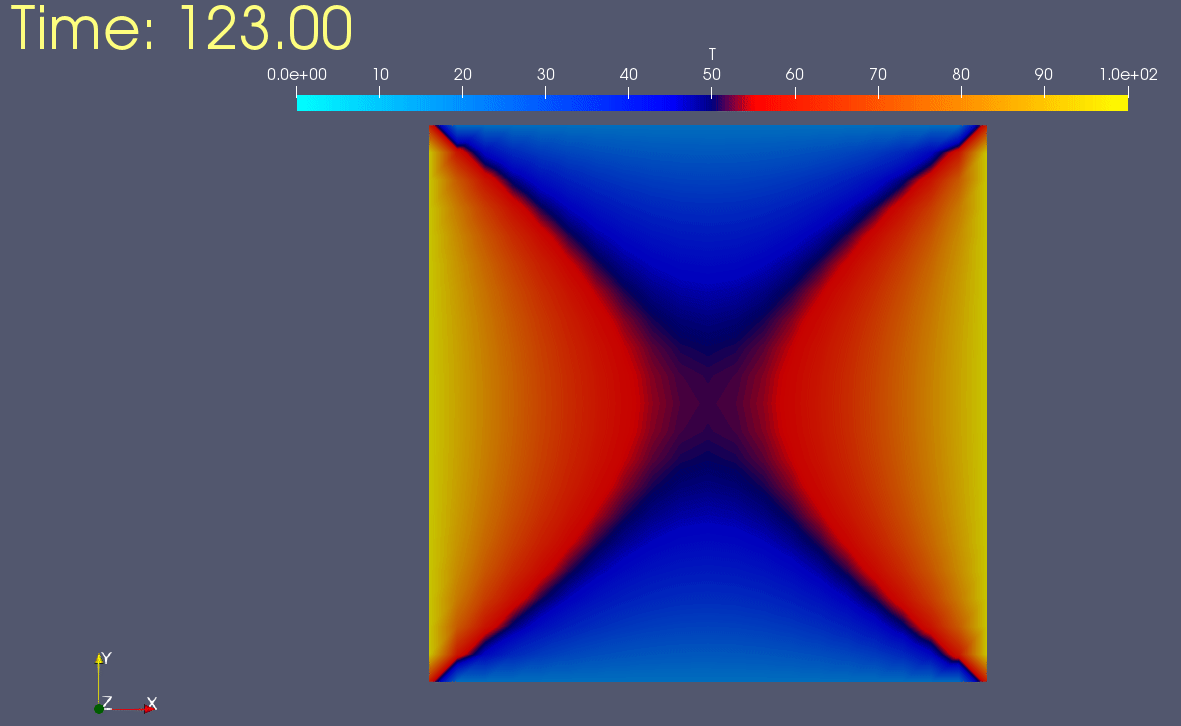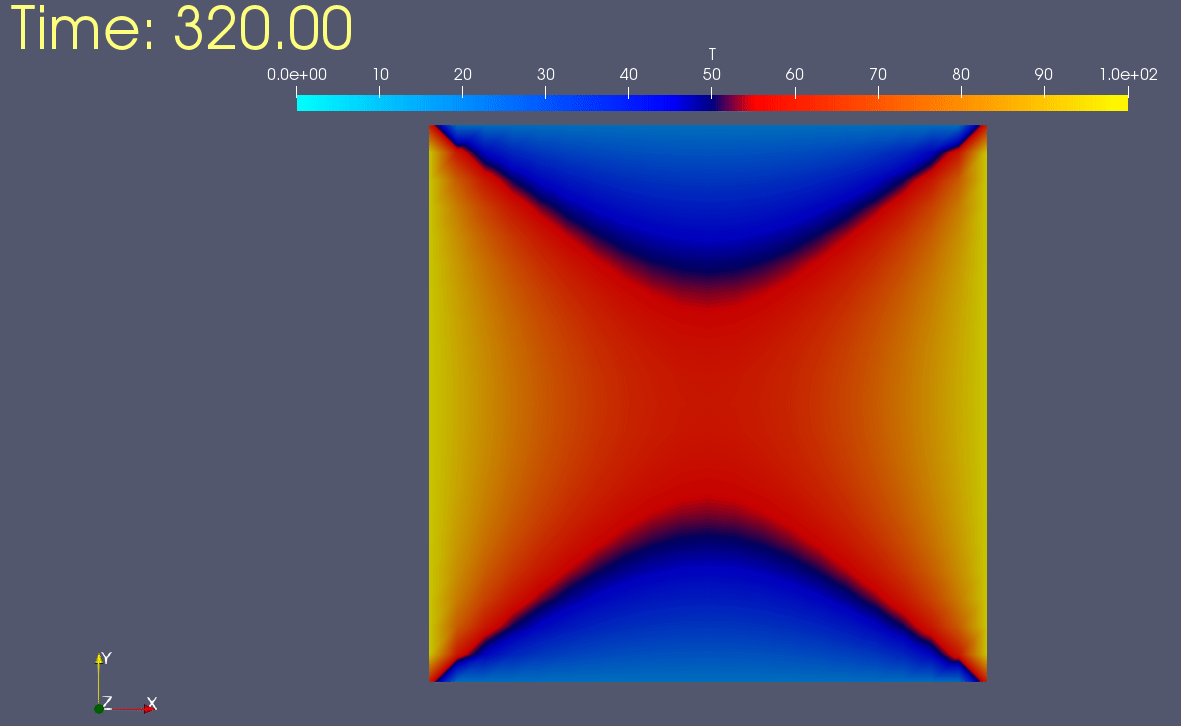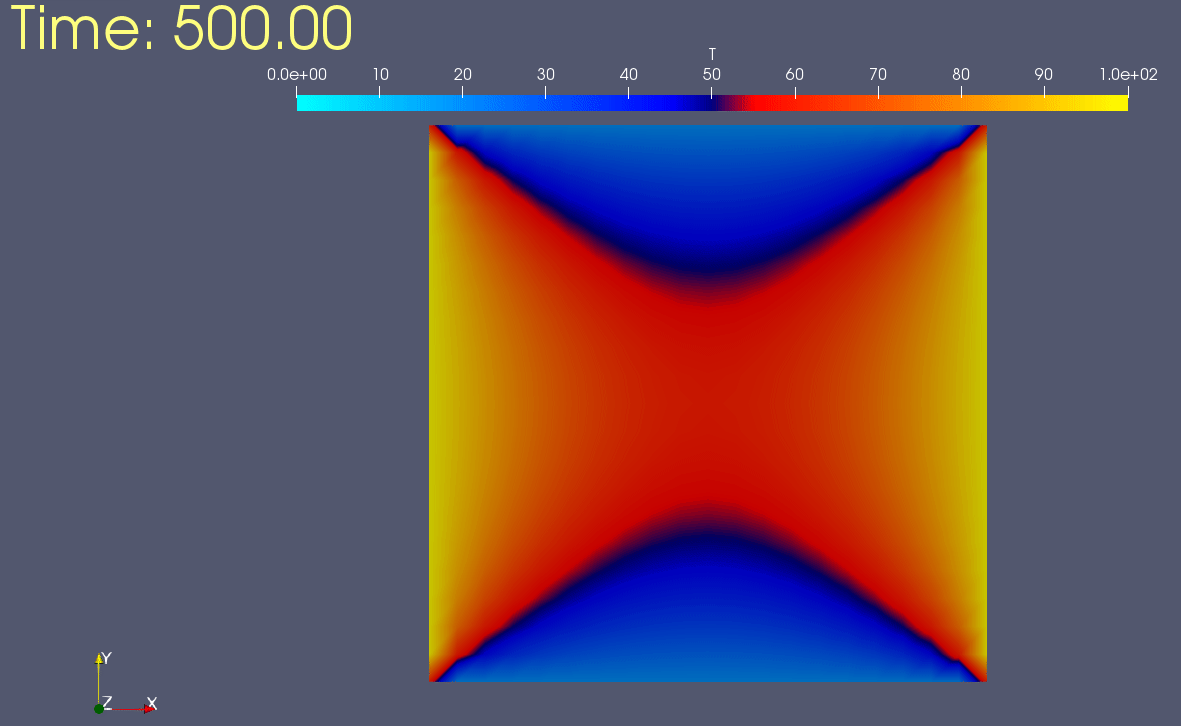
2ème cas:
(C.L): T(0,y,t) = 100 ; T(1,y,t) = 100 ; T(x,0,t) = 20 ; T(x,1,t) = 20.
(C.I): T(x,y,0) = 0.
Chauffage symétrique:
3ème cas:
(C.L): T(0,y,t) = 10 ; T(1,y,t) = 100 ; T(x,0,t) = 60 ; T(x,1,t) = 20.
(C.I): T(x,y,0) = 0.
Chauffage non symétrique:
Class:
Utilisation de logiciels libres
